Table of Contents
Portfolio Optimization¶
Now that we have a nice metric to evaluate Portfolio Allocations against each other, how can we optimize the portfolio holdings?
We could just guess and check a bunch of random allocations and see which one has the best Sharpe Ratio!
This is known as Monte Carlo Simulation.
We randomly assign a weight to each security in our portfolio, then calculate its mean daily return and std. dev. of daily return.
This allows us to calculate the Sharpe Ratio for thousands of randomly selected allocations.
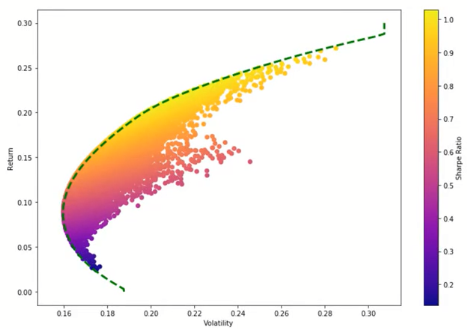
We can then plot the allocations on a chart showing return vs. volatility, colored by the Sharpe Ratio.
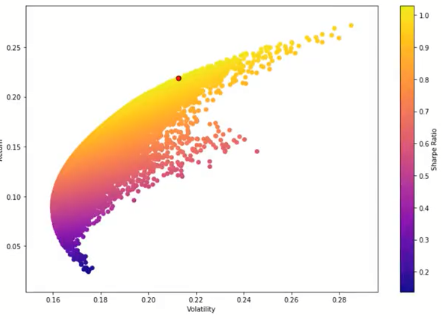
On the x-axis, we have the volatility. On the y-axis, we have the return. On the color bar, we have the Sharpe ratio. The red dot indicates the highest Sharpe ratio
Minimization¶
However guessing and checking is not very efficient, instead we can use math to figure out the optimal Sharpe Ratio for any given portfolio.
To understand optimization algorithms, we need to understand minimization!
Let’s say we are given simple equations:
- $y= x^{2}$
- $y = (2 - x)^{2}$
What value of x will minimize y?
- $y= x^{2}$ ----> x = 0
- $y = (2 - x)^{2}$ ----> x = 2
This idea of using a minimizer will allow us to build an optimizer.
Luckily for more complex equations, Python library SciPy can do the heavy math for us!
Referring back to our Sharpe Ratio, we want to actually maximize the Sharpe Ratio, meaning we can create an optimizer that will attempt to minimize the negative Sharpe Ratio!
We will use SciPy’s built-in optimization algorithms to calculate the optimal weight allocation for our portfolio (optimized by Sharpe Ratio).
The border is known as the efficient frontier